In this post I want to share with you: How to Copy a Metric Helical Gear from another one, that is, we are going to copy the data of a helical gear that we have to repair.

The steps are as follows:
- Count the number of gear teeth (Z)
- Measure the outside diameter of the gear.(Od)
- Take the angle of the outside helix.(oα)
- Calculate the approximate module. (aM)
- Calculate the helix angle.(α)
- Calculate the normal module. (M)
- Corroborate the calculations.
- Calculate the helix pitch or Lead of the gear. (L)
- Calculate the helix angle in the outside diameter.(oα)
Plus we’ll need:
- A Degree Protactor.
- A Rule,
- A Pen.
- A Pen Marker.
- A Sheet of paper.
Procedure for Copy a Metric Helical Gear :
Step 3: Taking the angle of the outside helix (oα):
Draw a straight line on the sheet of paper using the ruler and pen. This straight line will serve as a guide for placing the ruler on it.

Paint three or four gear teeth with the pen marker, to obtain the mark left by the gear teeth on the sheet of paper.
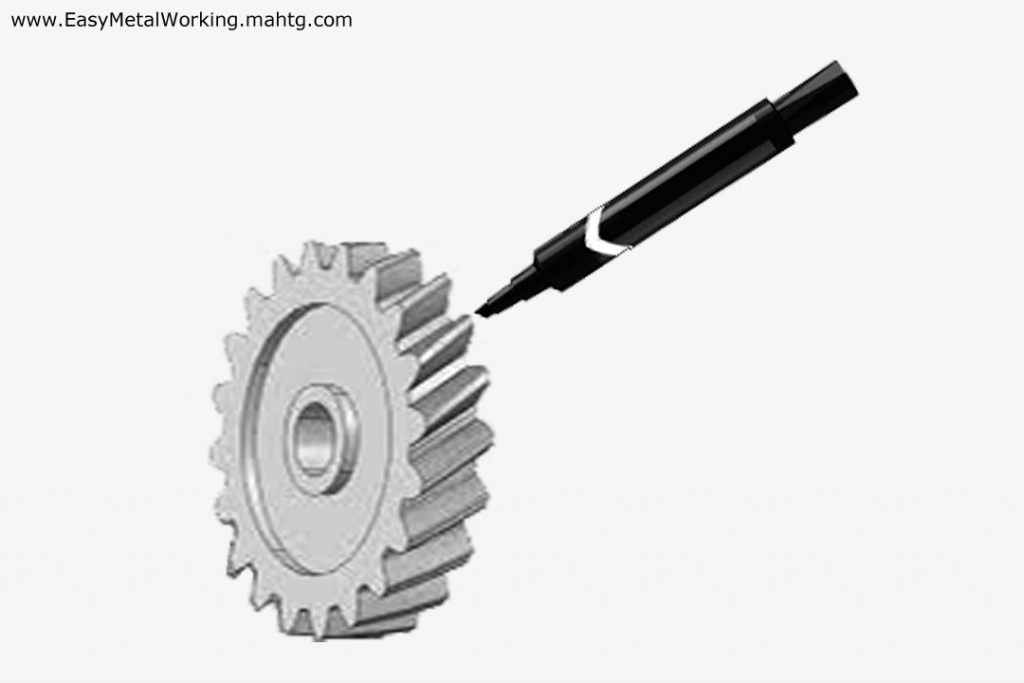
Place the gear on the sheet of paper and with the help of the ruler, exert a slight pressure and a forward movement in order to paint the gear teeth on the sheet of paper.
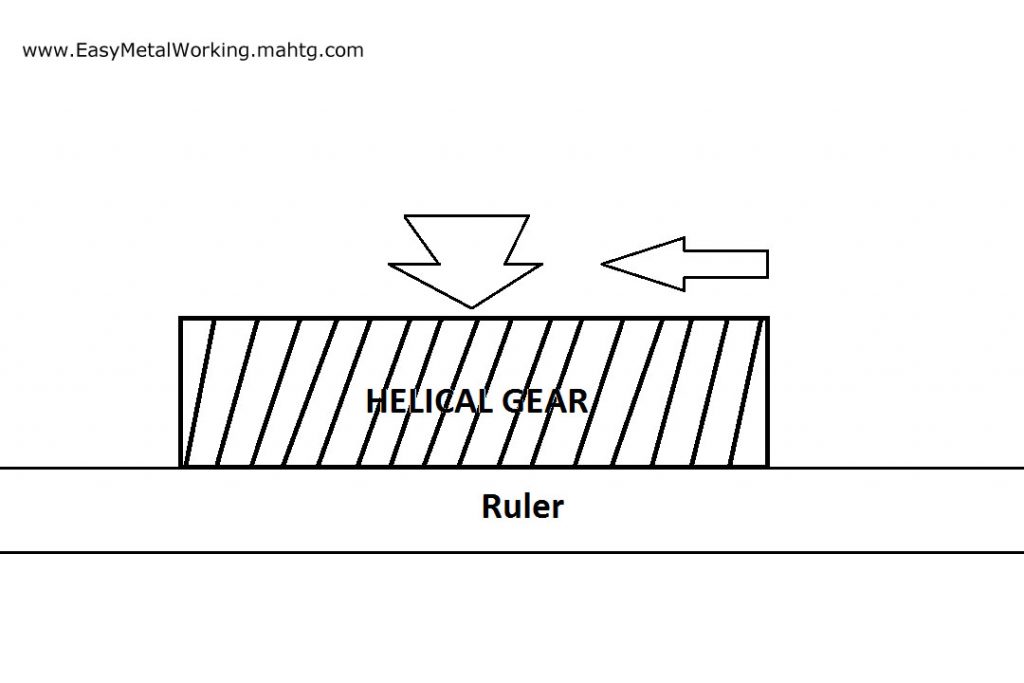
Extend the mark left by the gear teeth with the help of the ruler and the pen and finally, measure the angle with the degree protactor.
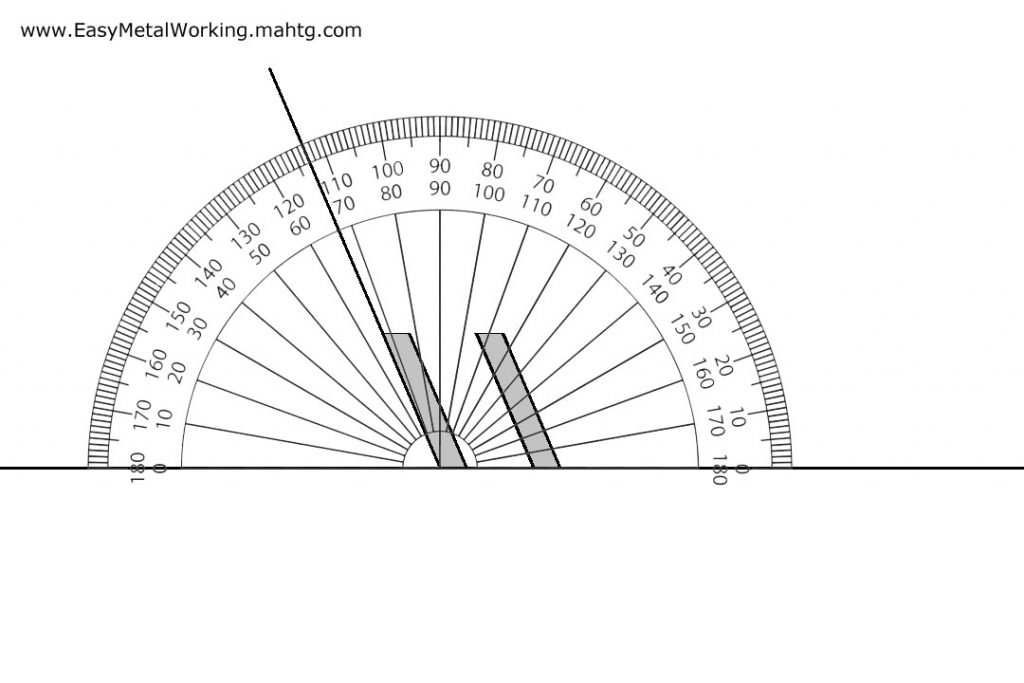
In this case the angle is 21°30′ approximately.
The helical gear in this example has the following data:
- Number of gear teeth (Z) : 25
- Outside diameter (Od) : 71.5 mm.
- Angle of the outside helix.(oα) : 21°30′
Now we have to calculate the approximate module. (aM), using the following formula:
aM = (Od/(Z/(Cos oα)+2))
Now, we must to replace the data in the formula:
aM = (71.5/(25/(Cos 21°30′)+2))
aM = (71.5/(25/0.930417568)+2))
aM = (71.5/(26.86965601+2))
aM = 71.5/28.86965601
aM = 2.4766
This value: 2.4766 is an approximate value of the module (M), but we need to find the value of the angle in the pitch circle of the gear that is the real value for the calculations, then with the following formula we can be very accurate and find the correct value of the helix angle:
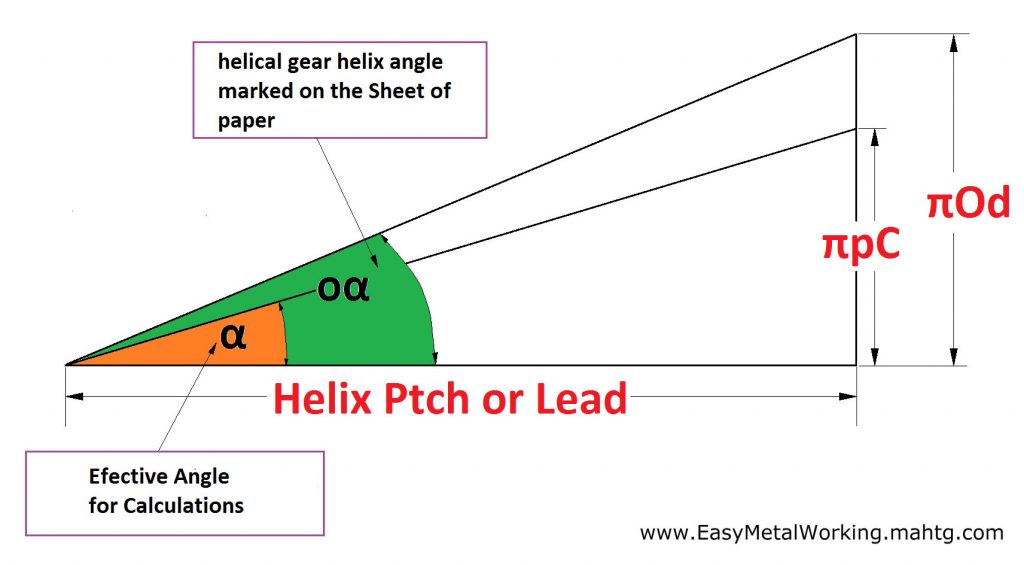
Tan α = (Tan oα (Od -2aM))/Od
Tan α = (Tan 21°30′(71.5 – 2(2.4766)))/71.5
Tan α = (0.393910476(71.5-4.9532))/71.5
Tan α = (0.393910476(66.5468))/71.5
Tan α = (26.213481664)/71.5
Tan α = 0.366622121
α = Arc tan 0.366622121
α = 20.1340536
So, this value is really equal to 20°
Finally, Alpha’s value is 20°
Now we can calculate the correct value of the normal module, based on the angle of the helix in the pitch circle, using the following formula:
M = (Od/(Z/(Cos α)+2))
M = (71.5/(25/(Cos 20°)+2))
M = (71.5/(25/(0.939692621)+2))
M = (71.5/(26.604444312+2))
M = 71.5/28.604444312
M = 2.499611572 really, Module is 2,5
Now, to corroborate that the calculation of the helix angle and the gear module are well done, we will calculate the helical gear with the data we just found; i.e. Normal module = 2.5; Number of teeth = 25; and Alpha = 20°, then:
Transverse Module (tM)
tM = M/cos α
tM = 2.5/cos20°
tM = 2.5/0.939692621
tM = 2.66
Pitch Circle (pC)
pC = tM(Z)
pC = 2.66(25)
pC = 66.51 mm.
Outside Diameter (Od)
Od = pC + 2(M)
Od = 66.51 + 2(2.5)
Od = 66.51 + 5
Od = 71.51 mm.
This data of the outside diameter corresponds exactly to the measurement that we take directly from the gear, whose diameter with the caliper is 71.5mm
Maybe you are interested in: How to Convert Millimeters to Fractional Inch Known
Finally, let’s calculate the helix pitch or Lead of the gear. (L):
L = Pi(pC)/tg α
L = 3.1416(66.51)/tg20°
L = 208.947816/0.36397023427
L = 574.08 mm.
Now, to be completely sure that the calculation is correct, we will calculate the the helix angle on the outside diameter of the gear, but already with the known data, that is, with the helix pitch, and the outside diameter of the gear.
tan α = π(Od)/L
tan α = 3.1416(71.51)/574.08
tan α = 224.655816/574.08
tan α = 0.39133189799
α = Arctg 0.39133189799
α = 21°22’18.84”
this value: 21°22’18.84” is the angle that we got with the degree protactor on the sheet of paper, but exactly.
I hope this information is useful and helpful to you.
If you liked the information you just saw, then rate me with the highest score in the stars section right below this post.
Thank you.